Why our puzzles are the best
To make puzzles we use the following, apparently contradictory, formula:
SIMPLICITY + SOPHISTICATION = PERFECTION
Simplicity – how to solve our puzzles is explained as succinctly as possible – the simpler, the better.
Sophistication – we combine true expertise and a real passion for puzzles with brand-new tools and state-of-the-art technologies.
Perfection – enthusiasts agree that the product of this simple sophistication is puzzling excellence.
Meet our collectables
 Preview
Preview
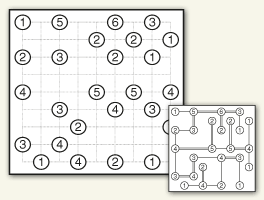
Bridges
The art of building bridges
Connect all of the islands with a series of bridges so that every island can be reached from any other island. Numbers indicate how many bridges can be built from each island. There are planning restrictions: bridges can be built only along the outlined network grid; no islands can be isolated; no more than two bridges are allowed between any pair of islands; bridges cannot intersect or be built across any island.
Featuring in #numbers: Collected
 Preview
Preview
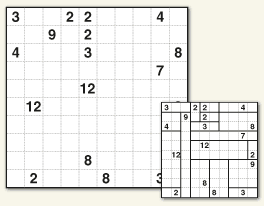
Cell Blocks
Break-out moments for the mind
Divide the grid into rectangles. Each rectangle must consist of the number of cells specified by the digit that it contains.
Featuring in #numbers: Concealed and #numbers: Collected
 Preview
Preview
Chain Link
Joined-up thinking, making the right connections
The set of numbers is defined by the size of the grid. A 5×5 grid will include the numbers 1‑5. A 9×9 grid uses the numbers 1‑9. Place each number once in each row and column.
In addition, each number appears only once in each chain.
Featuring in #numbers: Collected and #numbers: Engaged
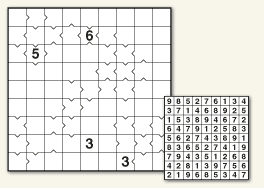 Preview
Preview
Futoshiki
Good relations, or the beauty of related numbers
The set of numbers is defined by the size of the grid. A 5×5 grid will include the numbers 1‑5. A 9×9 grid uses the numbers 1‑9. Place each number once in each row and column.
An inequality sign embedded in a border indicates that the number is larger or smaller than the number in the adjacent cell. Numbers separated by these signs are not necessarily consecutive.
Featuring in #numbers: Collected and #numbers: Engaged
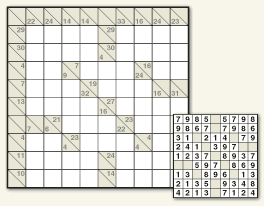 Preview
Preview
Kakuro
The art of logical deconstruction
A Kakuro is like a crossword or an arroword, except that the clues in tinted cells are sums.
Each answer must include only one instance of any of the appropriate numbers 1‑9 such that they add up to the sum (eg, if the sum is 4, the answer can be 1 and 3, but not 2 and 2).
Featuring in #numbers: United and #numbers: Collected
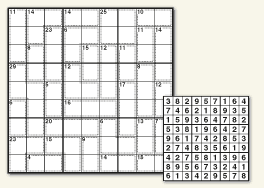 Preview
Preview
Killer Sudoku
Sudoku with Oomph!
Complete the puzzle by filling the grid with the numbers 1‑9 so that each row, each column and each 3×3 block contains all the digits from 1‑9. No single digit can appear twice in any single row, column or 3×3 block. In addition, there are bordered zones indicated by dashes, each with a value in its top-left corner. Numbers placed in each zone must equal the given value. No digit is repeated in a zone.
Featuring in #numbers: Squared and #numbers: Collected
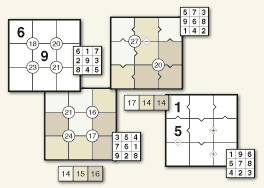 Preview
Preview
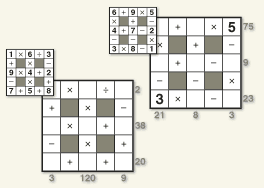
Nino
A tiny, shiny gem
Place each of the numbers 1‑9 in the grid. A number in a circle is the sum of the four surrounding cells. Similarly, a number in a tinted square is the sum of numbers that fit in the corresponding tinted area.
Inequality symbols indicate that a cell contains a number that is greater than > or less than < the number in the adjoining cell. (eg, 5>3, 2<5).
+ and − symbols indicate that the number in the adjoining cell is either one higher (+) or one lower (−). In puzzles featuring these symbols, all such instances are given.
Featuring across the full range of #numbers
 Preview
Preview
Set Square
Puzzles that add up
Place one each of the numbers 1‑9 in the grid to make sure all of the sums work.The conventional order of mathematical operations (BODMAS) does not apply. Sums should be solved from left to right, or from top to bottom.
Featuring in #numbers: Squared, #numbers: United and #numbers: Collected
 Preview
Preview
Sign In
The power of positive thinking
The set of numbers is defined by the size of the grid. A 5×5 grid will include the numbers 1‑5. A 9×9 grid uses the numbers 1‑9. Place each number once in each row and column.
In addition: + indicates the number immediately to the right or below is one higher. − indicates the number immediately to the right or below is one lower. All instances of consecutive numbers are shown by these signs.
Featuring in #numbers: Collected and #numbers: Engaged
 Preview
Preview
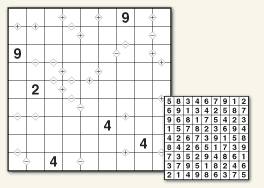
Slitherlink
The logic of twists and turns
Make a single undivided continent without lakes, islands or peninsulas. Draw lines along cell borders to form a single loop without crossings or intersections. A digit specifies the number of lines that border its cell. Empty cells may be bordered by any number of lines.
Featuring in #numbers: Collected
 Preview
Preview
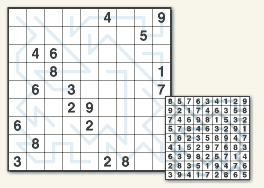
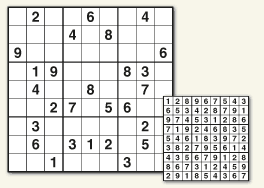
Sudoku
Know Sudoku? Think Again!
Complete the puzzle by filling the grid with the numbers 1‑9 so that each row, each column and each 3×3 block contains all the digits from 1‑9. No single digit can appear twice in any single row, column or 3×3 block.
Featuring in #numbers: Squared and #numbers: Collected
 Preview
Preview
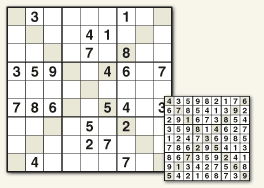
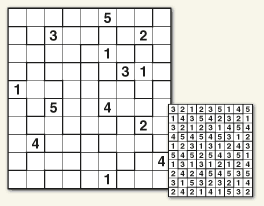
Sudoku‑X
Sudoku with the X‑Factor
Complete the puzzle by filling the grid with the numbers 1‑9 so that each row, each column and each 3×3 block contains all the digits from 1‑9. No single digit can appear twice in any single row, column or 3×3 block.
In addition, the tinted diagonals also contain the digits 1‑9.
Featuring in #numbers: Squared and #numbers: Collected
 Preview
Preview
Touch‑Me‑Not
The puzzle that stands alone
Complete the grid using the digits 1‑5. The number of cells in a block defines the numbers to be placed in it. For example, a block of three cells will contain the digits 1‑3. A digit can occur only once in each block. Identical digits cannot touch one another, even diagonally.
Featuring in #numbers: Concealed and #numbers: Collected
 Preview
Preview
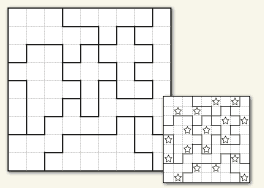
Twins
Reach for the stars
Every row, column and shaped area must contain two stars. These stars must be positioned such that they do not touch, even diagonally.
Featuring in #numbers: Concealed and #numbers: Collected